来源：微信公众号“KPMG大数据挖掘”

近年来，由人工神经网络研究发展出的深度学习（deep learning）算法被广泛运用于人工智能领域，在图像识别、机器翻译、智能机器人等方向取得了万人瞩目的显著进展。今天，喜爱神经科学的笔者将结合神经科学知识，以人工神经网络（artificial neural network）的基础算法多层感知机（multi-Layerperceptron）为例向大家介绍其原理。

大自然素来是我们学习的榜样。在物竞天择的法则下，生物不断演变，进化出精巧神奇的功能，为人类提供了丰富的学习素材。无论是《韩非子》中记载的鲁班用竹木作鸟“成而飞之，三日不下”，还是通过模仿翠鸟喙形状改进外形从而达到了降噪效果的新干线列车，人类的发展史中处处皆是人类视大自然为发明创造的灵感源泉之案例。

20世纪，随着人类对大脑认知的增加，一系列受大脑信息处理方式启发的算法应运而生，在一代代科学家日益秃顶的努力下，深度学习、人工神经网络的概念以围棋大王阿法狗AlphaGo的形象一举成名并广为人知，与佛系养生等文章一起，成为了微信朋友圈生态链的重要一环。

什么是人工神经网络呢？顾名思义，人工神经网络是指借鉴了生物大脑神经结构的运算模型，它们运用了生物神经元的抽象概念，参考了其根据环境而学习的能力，以此为基础进行一系列复杂运算，相比许多其他类型的机器学习算法，能够更好得解决多变量分析问题。

1 生物神经网络

为了获悉人工智能网络是如何借鉴生物大脑的，先让我们了解一下真的神经元。

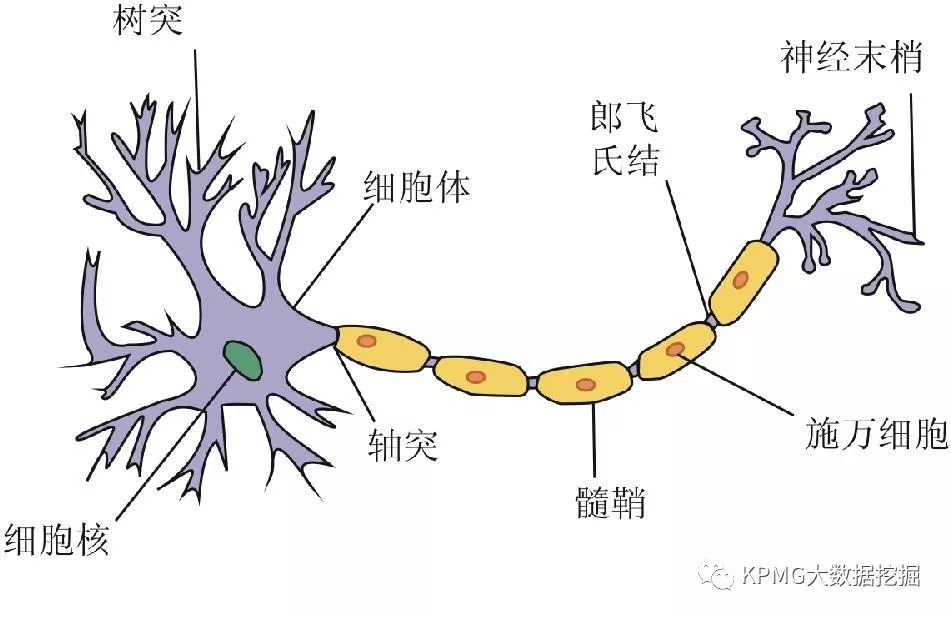
从图中，我们可以看到神经元有两个重要的组成部分：树突（dendrite）和轴突（axon）。树突非常繁杂，分布广泛，能够接受来自于不同细胞（尤其是其他神经元）的输入信号；轴突则只是长长一条，向外延伸，为神经元的输出端。

上述中拥有输入输出功能的神经元，在人类大脑中约有1000亿个，它们是如何传递、处理信息的呢？简单来说，树突接收到的输入信号会影响神经元细胞膜内外离子的流动，改变细胞内外的电位差，当改变累积到一定程度时，神经元会产生局部兴奋，而轴突便会沿着自己长长的身躯，将兴奋以电信号的方式传递出去（该电信号称为动作电位，Action Potential），从而输出信息，再改变其他神经元的膜电位。这一过程可以参考下图，图中展示了神经元在接收到不同输入信号后的反应。

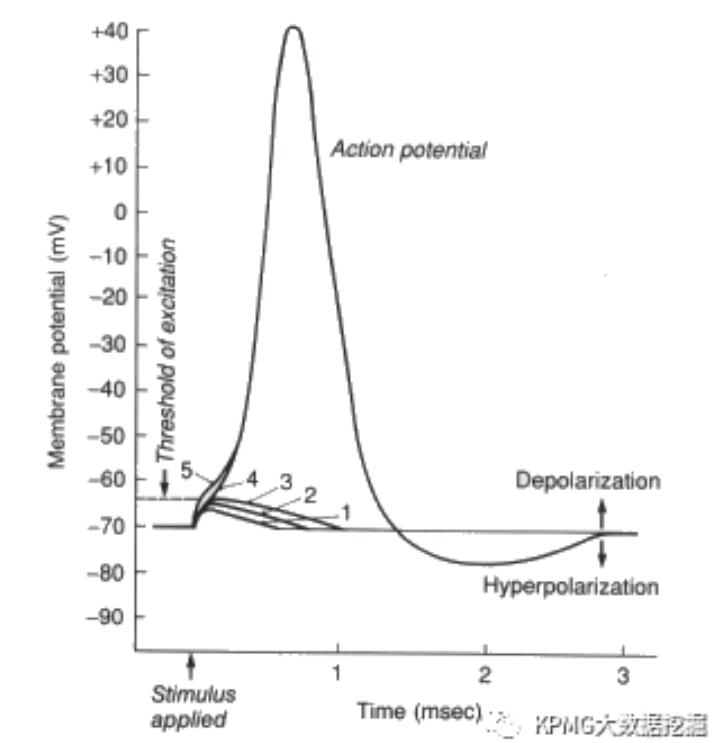
如图所示，在1-3的情况中，由于输入信号较弱，电位差改变太小，没有达到神经元的兴奋阈值，因此没有出现动作电位；在4-5的情况中，膜电位达到阈值，动作电位产生。值得注意的是，即使情况5比4的膜电位要高，两者产生的动作电位强度相同——事实上，这并非偶然，在到达阈值后，每次产生的动作电位强度都是一致的。

至此，我们可以清楚地看到，神经元的输入输出关系是非线性的——从数学的角度来看，就像是一个开关函数，达不到阈值，则输出为0，达到阈值，则输出为1。

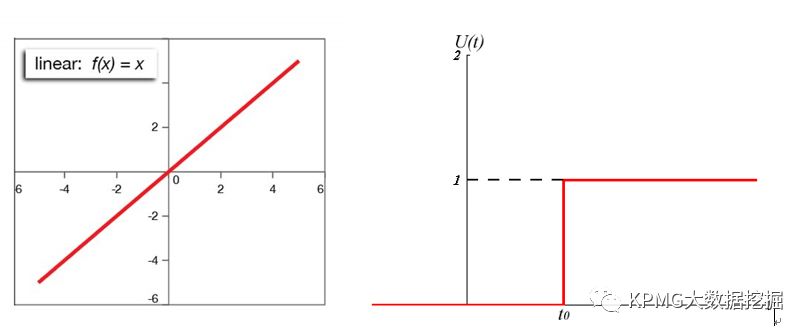
线性函数（左图）和开关函数（右图）

现在，我们已经获悉神经元互相沟通的方式啦~那么，人脑能够根据经验而不断学习的这一技能的生物基础是什么呢？

1949年，加拿大心理学家唐纳德·赫布（DonaldHebb）受巴普洛夫实验的启发，对这个问题的答案提出了猜想。赫布律（Hebbian theory）认为同一时间被激发的神经元间的联系会被强化，从而形成一个细胞回路。这一假设为神经元的学习机制提供了正确的理论方向。

1966年，神经元长时程增强效应（Long-termpotentiation）第一次在实验中被发现，为赫布律提供了神经生理学基础。长时程增强效应形容了一种现象，即，如果神经元A曾持续高频地令神经元B发出动作电位，那么神经元B就会更容易被神经元A激活。

导致这一现象的机制有很多，其中一种模式是，在被神经元A多次激活后，神经B靠近神经元A轴突的树突中会增加更多的接收器，从而提高接受神经元A输出信息的效率；同时，神经元A也会释放出更多的神经介质，从而更大程度地影响神经元B的膜电位，让其比之前更易激发。

从数学的角度，我们可以理解为，在神经元A多次导致神经元B放电后，神经元A对于神经元B是否会被激发的影响权重长期性地增强了。在我们的生活中，学习是指“人在生活过程中，通过获得经验而产生的行为或该行为潜能的相对持久的行为方式”，与其定义类似，在大脑的微观世界中，神经元时时刻刻进行着同样的行为。

图中展示了一个神经元的轴突（浅蓝部分）和另一个神经元的树突（浅紫部分）。其中，左图为多次共同激发前，右图为多次共同激发后，可以看到右图中接收器和神经介质都发生了增加，表明两个神经元之间的联系增强。

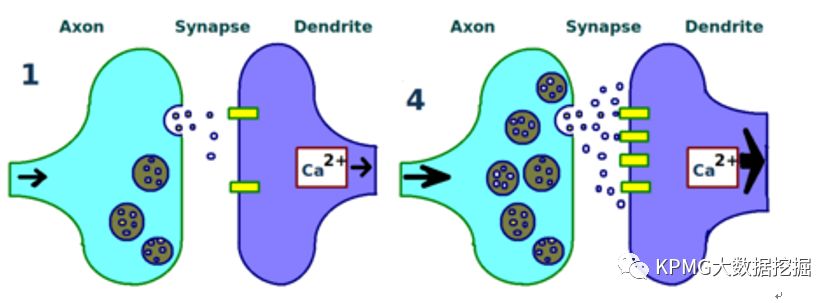
现在，我们已经认识到神经元具有输入输出功能，并能够相互沟通；沟通时，输入与输出信号之间的关系是非线性的；高频沟通之后，神经元之间的影响权重会发生改变影响。为了简化关系，我们在解释的过程中只描述了两个神经元之间的互动，然而在大脑中，神经元之间有着多对多的联接关系，信号也可以被一层层地传递出去。而人工神经网络的发展，正是借鉴了大脑神经系统的这些特质。

大脑中互相影响的神经元示意图，图片来自互联网。

2 人工神经网络

人工神经网络是受人脑处理信息方式启发的计算模型。在人工神经网络模型中，最基本的运算单位是神经元（neuron），又称为节点（node）。由于本文将展开生物与人工神经网络的对照，为了区分概念，本文中笔者将人工神经网络的基本单位统一称为节点。

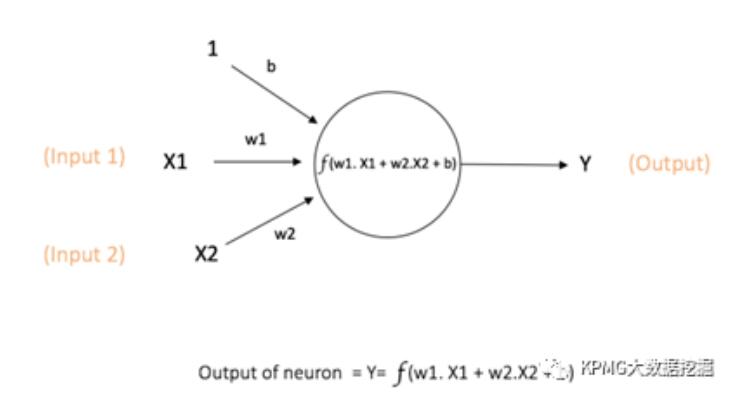
节点示意图，图片来自互联网。

如上图所示，与神经元类似，节点也会能够输入、输出信号。在将与之相连的输入信号（图中的1，x1，x2）乘以其对应的不同权重（图中的b, w1, w2）后，节点会对它们求和，输入其预先设定的激活函数（activation function），再转化成输出信号（图中的y）。

就像神经元的信号转换是非线性的，激活函数也同样是非线性的，以此来模拟更为复杂的关系。其中常用的一种是Sigmoid函数。

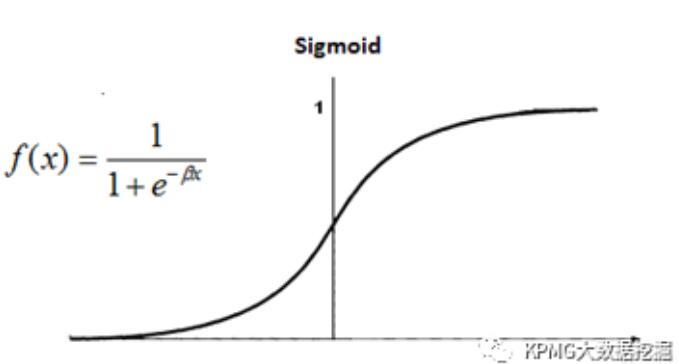
Sigmoid函数，图片来自互联网。

我们知道，大脑处理信息的优秀能力主要源于神经元之间的沟通，那节点之间是如何联接的呢？我们将以多层传感器为例，对此展开说明。多层传感器是前馈神经网络（feedforward neural network）的一种，后者是最基础也是最先被发明的神经网络算法。

在前馈神经网络中，节点以层的形式排列，并与其上下层的节点相连。某种程度上，我们可以把某个节点连接的上层节点视为向该神经元进行输入的神经元，其连接的下层节点当成接受该神经元输出的神经元。由于叫做“前馈”神经网络，不难想象，信息的传递是单向的，以层的方式向前递进。

网络的第一层节点被称之为输入层，用于输入特征向量，最后一层节点被称为输出层，用于输出预测结果。任何输入层和输出层之间的层被称为隐藏层，隐藏层既不直接接收外界的信号，也不会直接输出信号。最简单的前馈神经网络的隐藏层层数为零，被称之为单层传感器（single layer perceptron）；隐藏层数不为零的前馈神经网络，则是我们关注的多层传感器。其中，隐藏层数大于一的多层传感器，被称之为深度神经网络。

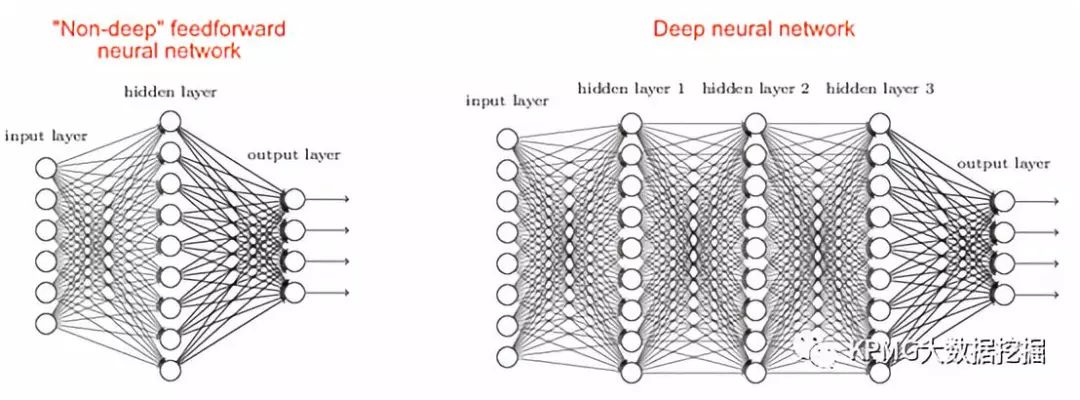
两个多层传感器的图例：左图是非深度前馈神经网络，右图是深度神经网络。图片来自互联网。

那么多层传感器具体是如何运作的呢？与传统的机器学习的目的相同，我们使用计算模型的目的是为了根据输入值来预测输出值。

上文已经提到，节点之间的联接存在着不同的权重。以权重值为变量，描述输入数据的预测值和实际值差异的函数的叫做损失函数（cost function），有不同的定义方法，其常见的二次函数形式为：

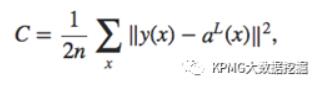
y（x）指已有数据的实际结果值，a^L（x）指输出层的预测结果值，n是数据总数。可以看到，损失函数在任何情况下都是非负的，当预测精准到与现实值完全相符时，C=0。而我们的目的，也就是调整损失函数的自变量，即多层感知器中的各个权重，将损失函数最小化。

显然，此处轮到梯度下降（gradient descent）登场了。众所周知，函数的梯度是一个向量，描述了面对函数自变量（输入值）发生相同距离的极小改变时，使函数因变量（输出值）发生最大改变的方向，因此，如果我们向其反方向移动，便可以最有效率地最小化函数（当然，会有锁定在极小值的问题，但从实践结果来看，通常梯度下降能够取得足够好的结果）。

没有相关数学基础的读者，可以将这个过程想象成爬山。以爬山的目的是达到山顶的高度为前提，在理想情况下，我们当然希望是能够原地起飞，垂直上升的……然而，不是每个人都是小仙女/小仙男，受到地心引力的限制，我们只能依赖爬山。

沿着山有很多走法（可以绕着山路一圈圈走，也可以一会儿绕着顺时针圈走一会儿逆时针走，回到原地），我们希望能找到使自己最快达到山顶的方向（也就是连接你到山顶的那条直线所指的方向）。显然，随着我们的位置变化，这个方向可能是会随时改变的。

每一条路都对应了一种调整自变量的方式，而这个能使你最快到达山顶的路的方向就是函数梯度所揭露的信息，它随着你所处的位置而改变。因为我们的目的是将损失函数最小化，所以在求出上山最快方向之后，我们选择了向其反方向行走，相当于获得了最快下山的路径，故称之为梯度下降。

于是，我们的核心问题就变成了如何计算梯度。最直接的方法是对每一个自变量求偏分，可由于这样子计算量过大，以至于优化结果很一般，多层传感器的实践一度陷入僵局，直到1980年代，反向传播（backpropagation）算法被运用在梯度计算当中，使其能被更高效地计算出来之后，深度学习才迎来了新的突破。

运用了反向传播的多层传感器大概以这样的方式计算：起初，所有的权重都被随机地赋予一个初始值。每当有一个数据输入，模型都会根据已有的权重产生一个输出值，我们将计算损失函数求关于输出变量的偏分，代入已知和预测的输出值，作为预测的误差值，通过链式法则，将其一层层地返回上层，计算出损失函数的梯度，以此调整权重，并重复以上步骤，直到误差小于提前规定的阈值。

想要阅读反向传播数学原理的读者，可以参考在线教材“Neural Networks and Deep Learning”（http://neuralnetworksanddeeplearning.com/chap2.html），文章中给出了较为严谨的证明，同时讨论了定义损失函数需要注意的前提条件等问题。

以上，大概就是笔者对于多层传感器计算原理的介绍啦~ 虽然上文中提及了很多人工与生物神经网络的相似之处，但笔者想要强调一下，人工神经网络仅仅是受生物神经网络启发而生，而并非与其机理完全相同。比如，为了方便梯度下降的运算，激活函数通常是连续可导的，而并非是更符合神经元处理信息模式的开关函数。

此外，值得一提的是，人工智能网络的完善，某种程度上也启发了我们探索自身大脑的方向。比如，人们曾一度认为神经元之间的信号传递是单向的（动作电位从轴突传递出去，影响下一个神经元），并不存在反向反馈给上一个神经元的机制与可能性，但是笔者在为这篇文章准备材料的时候发现，反向传播算法在人工神经网络的运用，引导部分神经科学家探索起了人脑反向传播的可能性；近年来，也发现了动作电位向树突传递的证据，即使其功能依然广受争议，但这种冥冥之中、若有似无的联系还是让笔者觉得非常神奇。

阅读至此，相信大家对于人工神经网络的原理，以及它和生物神经网络的联系，已经建立了初步的理解。当然，算法和自然碰撞的灵感火花数不胜数，人工神经网络与生物神经网络相互启蒙的故事依然尚未完结。随着神经科学不断发展，我们对大脑运作模式的理解随之加深，未来会发生什么？想想也是有些期待呢~:D